How do you know whether something is a trend or not? First, we need to define a trend. A trend is:
a general direction in which something is developing or changing
Second, we should mathematically define and be able to detect a trend. Trend analysis (and any kind of statistical analysis) is generally not something we can do by looking at the data or a visualization of it unless the data is overly simple; for what most marketers and business folks mean when they talk about finding trends, you need to do the analysis mathematically.
Here’s an excellent definition of when a trend is statistically meaningful, by the USA National Institute of Health:
If one or several regressions concerning time and values in a time series, or time and mean values from intervals into which the series has been divided, yields r^2≥0.65 and p≤0.05, then the time series is statistically meaningful.
That’s a great, concrete definition of a trend, something we can understand and implement. But what does it mean?
A Deep Dive Into What is a Trend
Let’s break the NIH definition down, for those folks who need a quick refresher. A regression is, in its simplest incarnation, fitting some kind of line or curve to our data that explains our data in some way. Suppose we had a chart that looks like this:

And we try to slap a line on it:
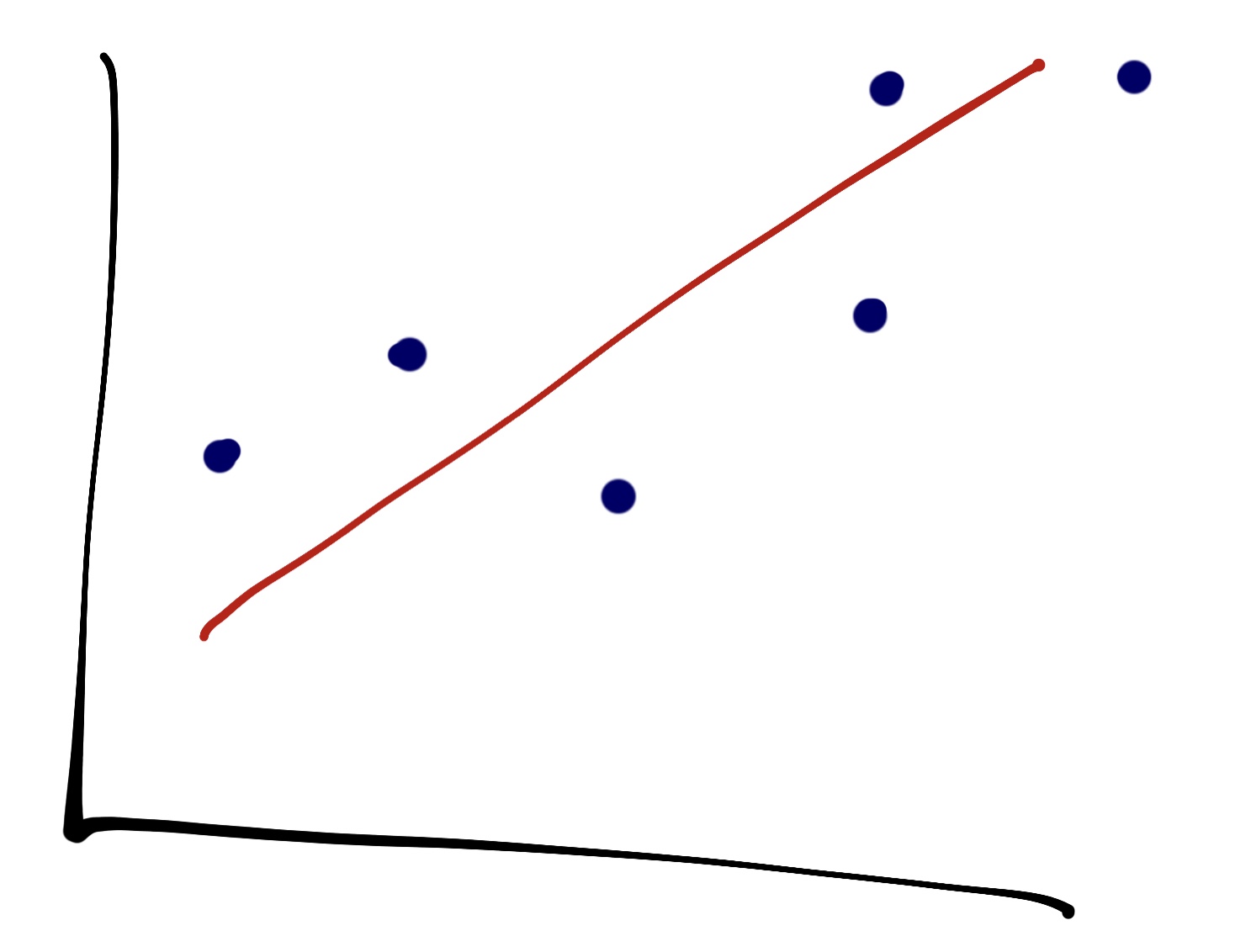
That’s the simplest form of regression: trying to find some kind of mathematical relationship among our data. In this example, we see a linear relationship between the x and y axis, visualized by the red line. As one variable goes up, so does the other one. That’s a trend.
Now, is this trend meaningful? This is where we turn to our definition and the mathematical concepts embedded in it – r^2 and p-values. The metric r^2 means how closely our trend line fits the data, and is measured from 0 to 1.
A very low r^2 looks like this in a linear regression:
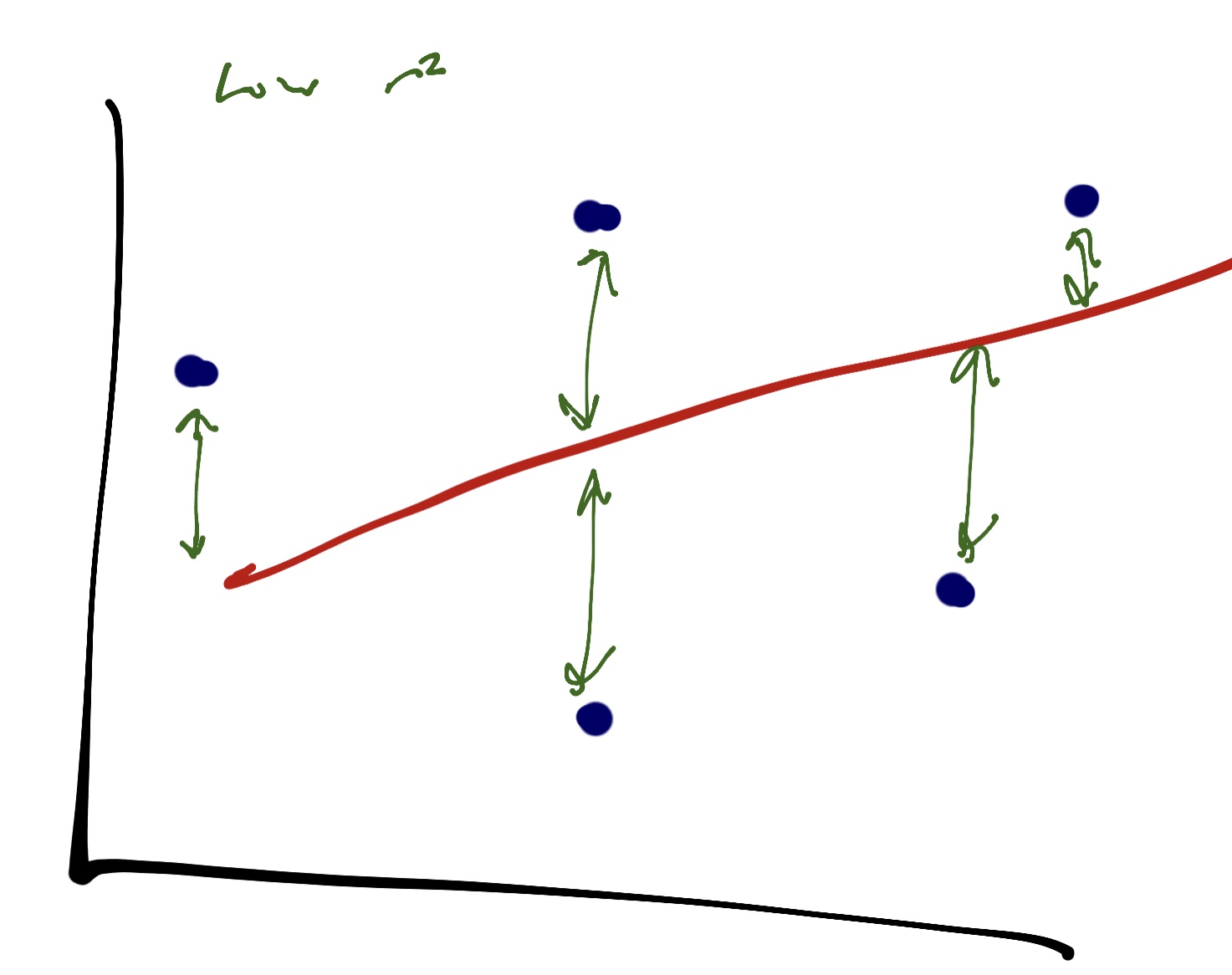
We can see that there’s a lot of distance between each point and the line describing it. If that distance is really big for every point, it likely means our trend isn’t meaningful; our line doesn’t do a very good job of explaining the relationship.
An very high r^2 looks like this in a linear regression:
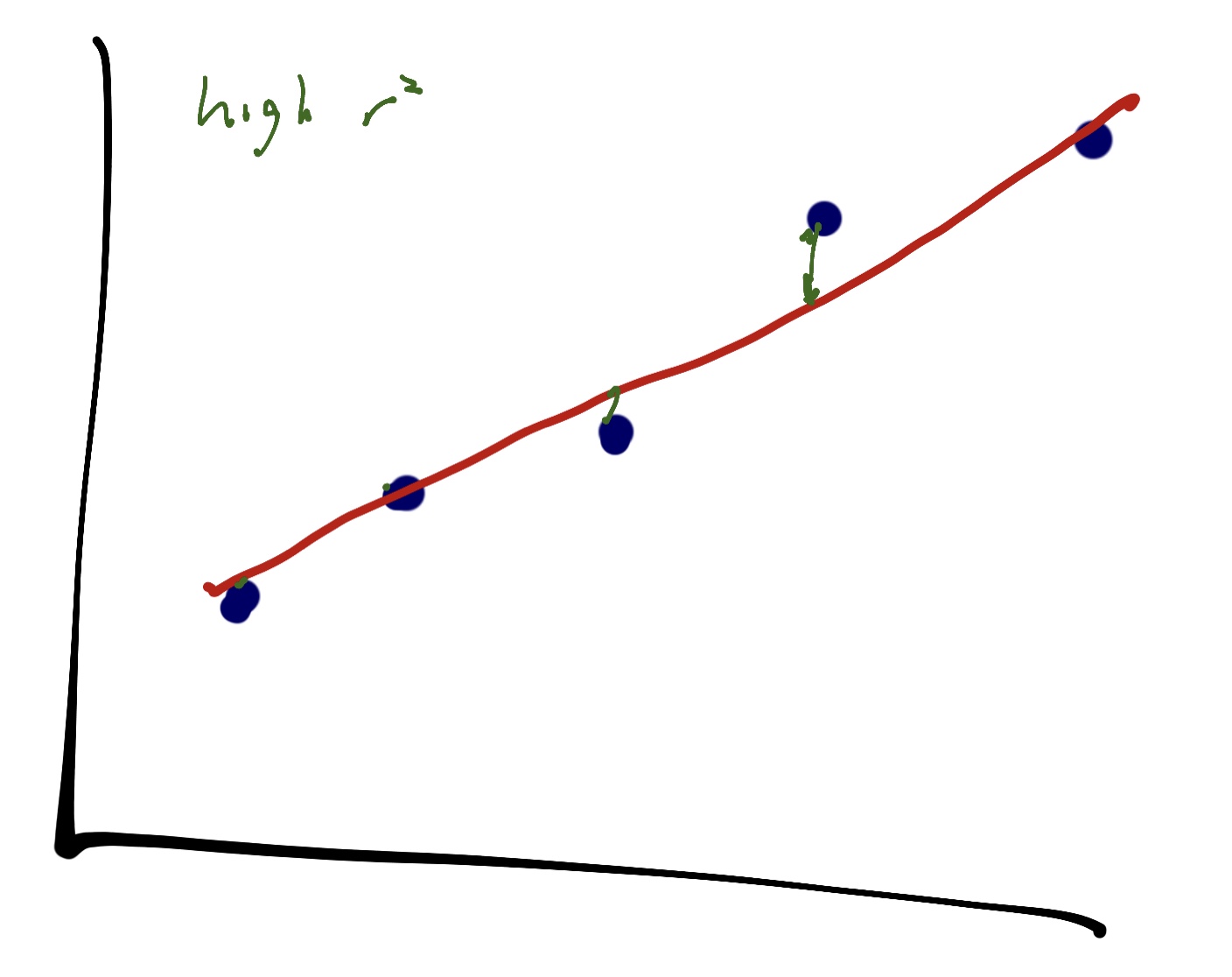
We can see that there’s very little distance between the points and the line. The line does a really good job of explaining the relationship in the data.
The p-value measure is a measure of how probable the null hypothesis is. In our example, our hypothesis is that there’s a trend of some kind. Our null hypothesis is that there’s no trend at all.
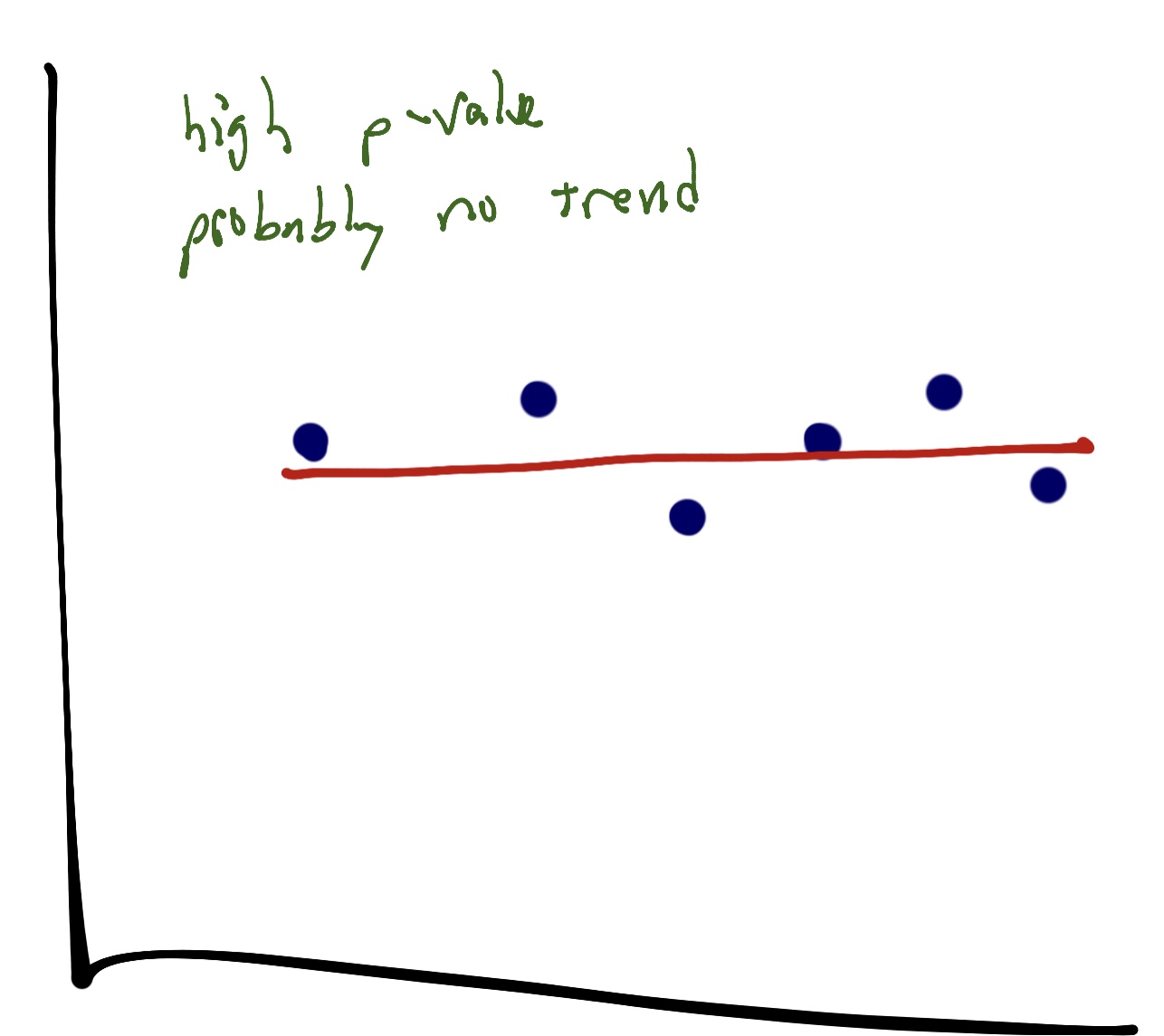
For example, in this chart, the line is flat, which would indicate no relationship between the data:
Compare that with this chart, where there is clearly a trend. The p-value would be low:
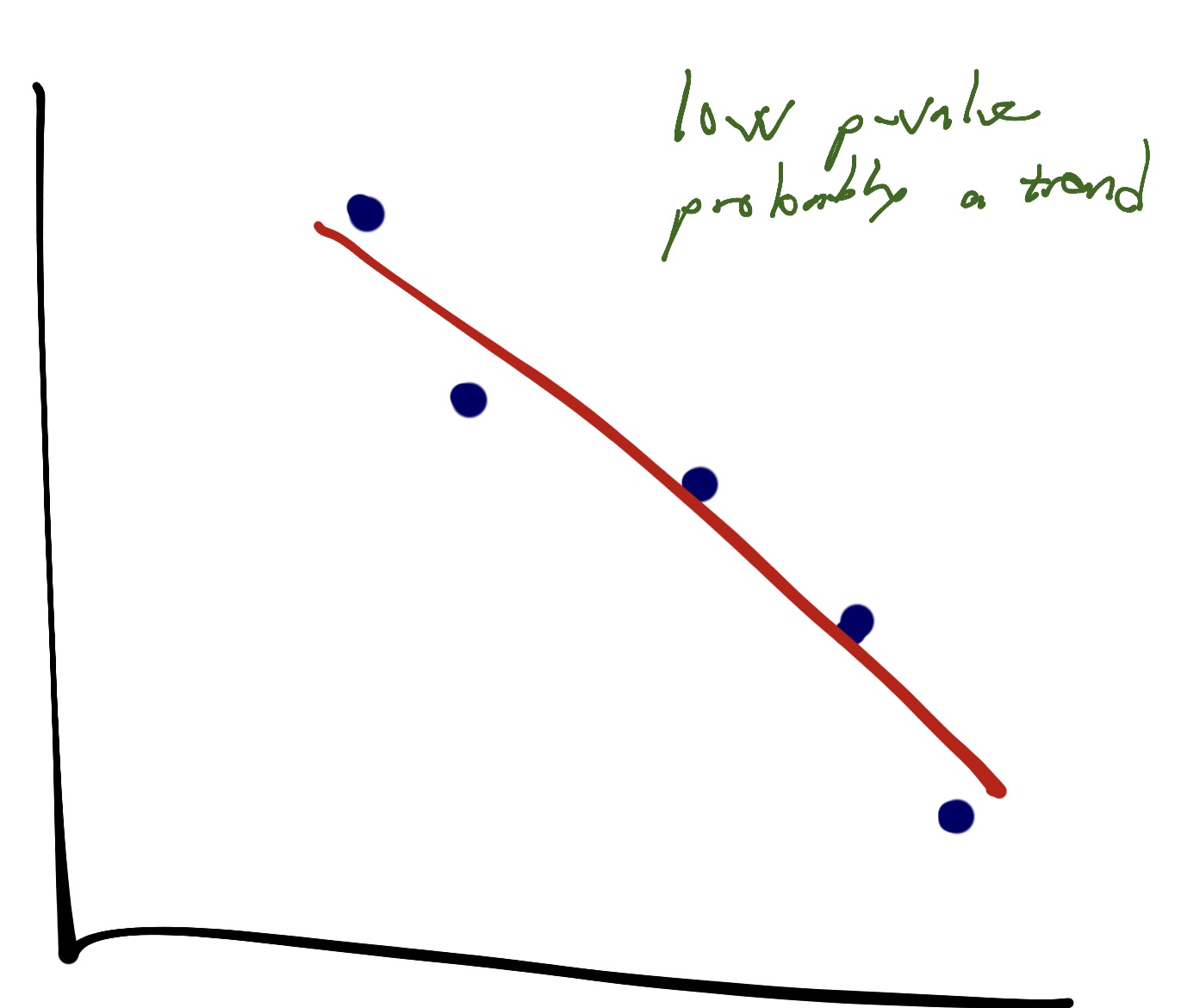
That’s how we determine whether something is mathematically a trend or not. We have to ascertain whether there is a relationship (by p-value) and the regression describes the relationship is described well by the data (r^2).
Where do these measures come from? Statistical software like SPSS and R will automatically produce them when you do regression in them. They won’t necessarily have an attractive graph or chart (you have to produce that separately) but they will give you the data you need to make an assessment.
There are a number of advanced statistical techniques (literally dozens of different kinds of regression) that we could use to evaluate whether something is trending or not, but they all follow these general guidelines – is there a trend, and how reliable is our prediction of the trend?
A Trend Analysis Walkthrough: Tiktok
So, with the basics of trend identification out of the way, let’s look at an application of the concept. We’ll use data from a service like Google Trends. Let’s pick something simple, like the number of people searching for the social networking app Tiktok over the past 5 years:
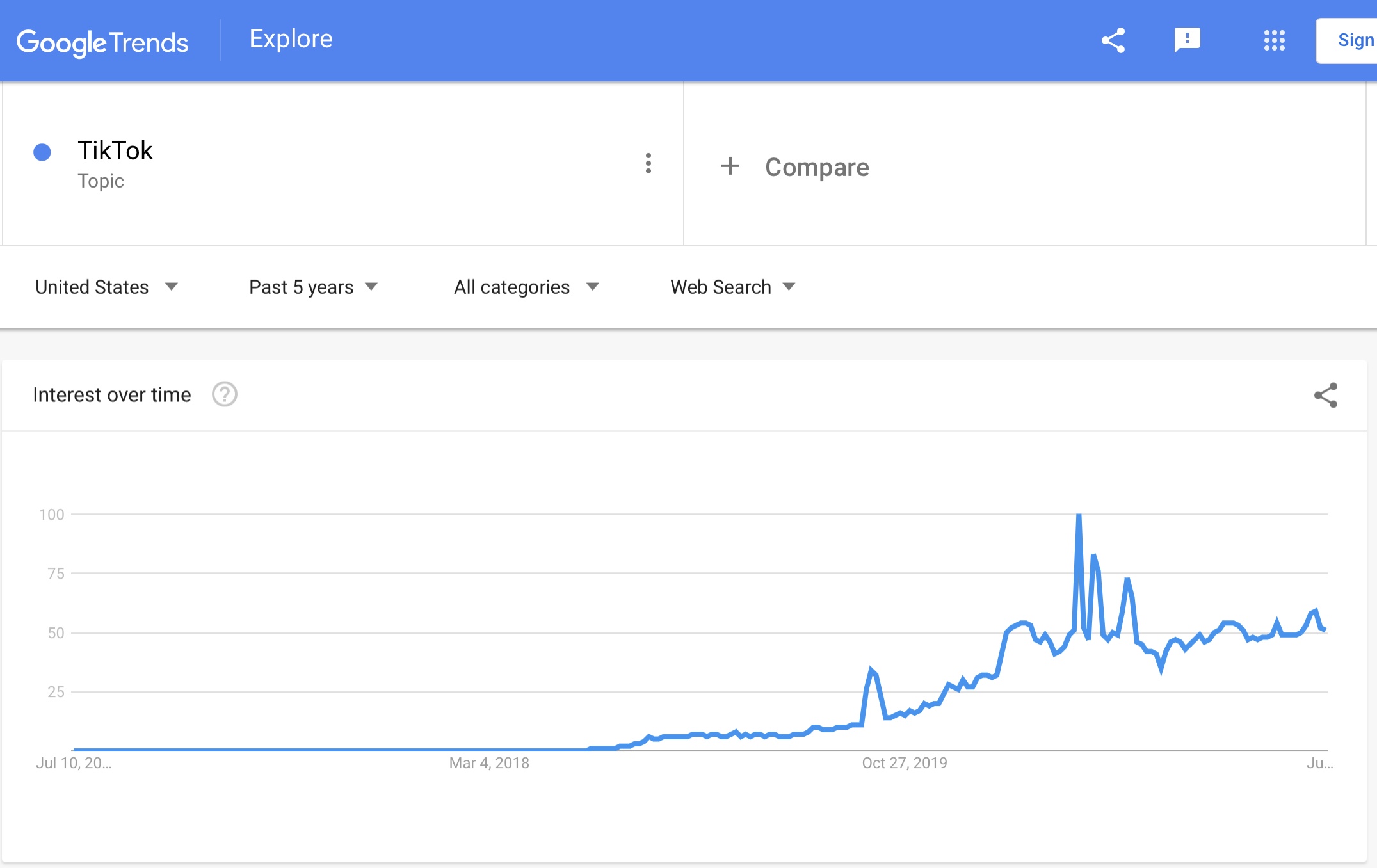
So the question is, is there a trend here?
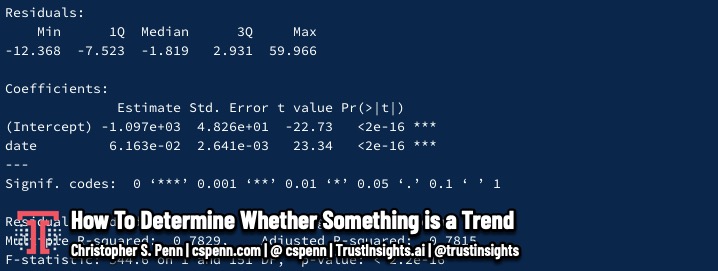
If we perform a linear regression, we get these results:
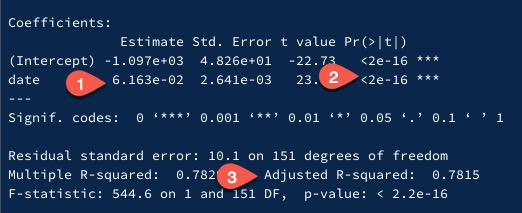
What do these mean? Point 1 shows the progression of the trend, the increase happening over time. Point 2 shows the p-value, which in this case is extremely small, indicating that the chart above shows a strong trend. Point 3 is the r^2, which is fairly high, indicating that the trend we’ve detected may be statistically meaningful.
So, in the last 5 years, is Tiktok a trend? We would answer yes. It meets the conditions set by NIH’s example of an r^2 > 0.65 and a p-value < 0.05. It’s a trend.
But, what if we look only at the last year?
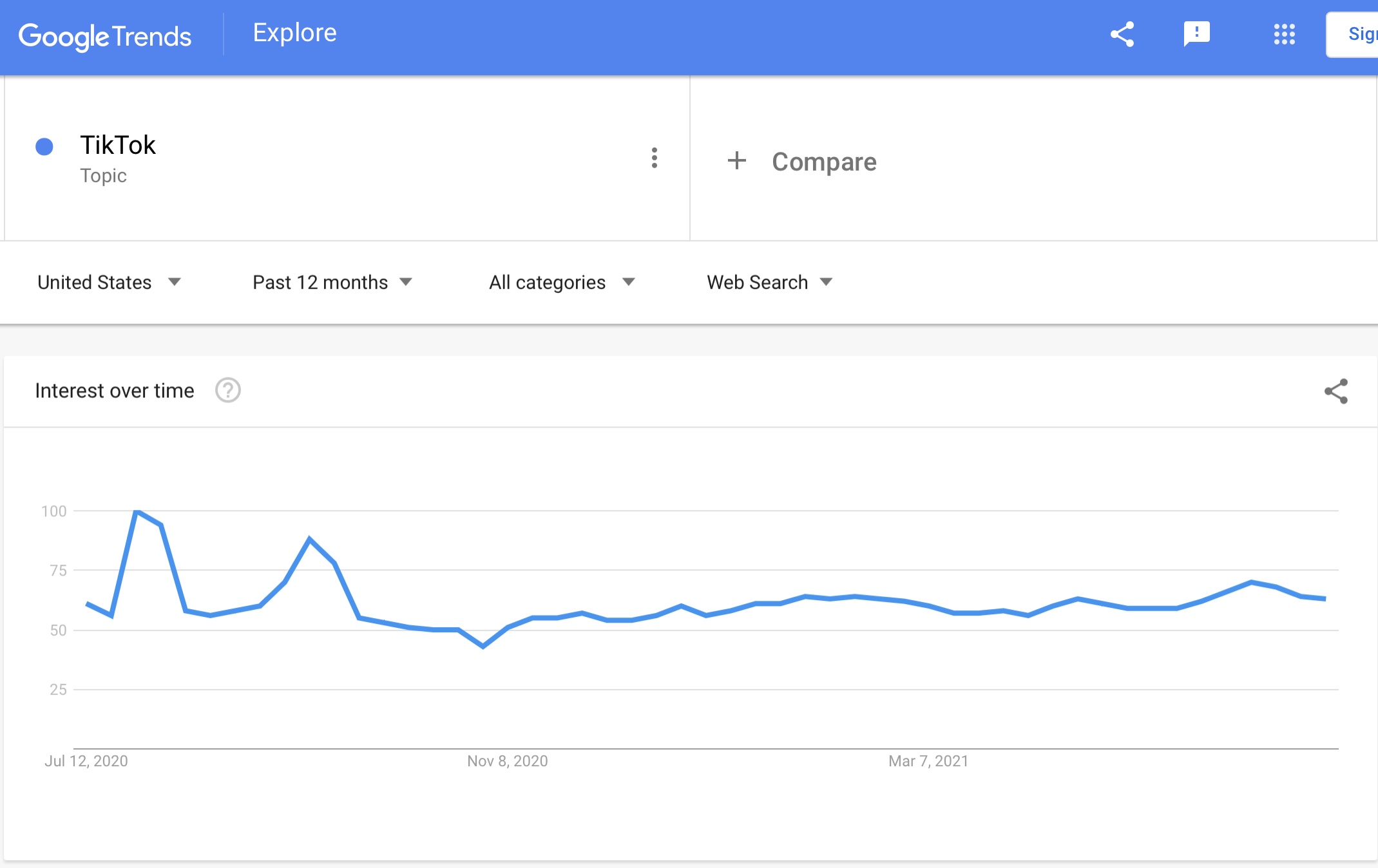
Let’s re-run the exact same test.
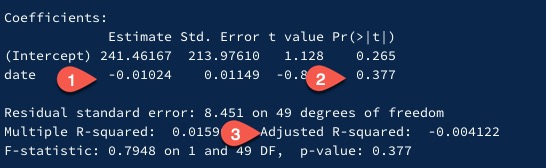
Here we see the lack of a progression at point 1; as date progresses, we see searches actually decline. We see a p-value well over 0.05 at point 2, 0.377. And we see an r^2 of almost zero, which means that our data is poorly explained by our linear regression.
In other words, in the last 52 weeks, is Tiktok a trend? We would answer no, at least in terms of basic linear regression. It doesn’t meet the conditions set by NIH’s example of an r^2 > 0.65 and a p-value < 0.05. It’s not a trend. Is it still relevant? Perhaps – but mathematically, it’s not a trend for the last 52 weeks.
Is Tiktok a trend or not? In the macro picture, yes. In the shorter-term, no. What do we do with that information? If you were trying to evaluate whether Tiktok was something you had to jump on for early adopter advantage, the lack of a trend in the last year would indicate that window has closed.
What About…
The big question marketers always have is whether or not X or Y is a trend they should be paying attention to. Whether it’s NFTs, MySpace, the Internet itself (remember the days when marketers said the Internet was a fad?), or any other topic, marketers generally want to know whether something is a trend or more important, whether something is likely to be a trend.
In this article we walked through the math behind what is a trend or not, along with an example. Any time you’re evaluating a time-based data series, apply the NIH definition and the statistical test to it. If it passes the test, it is mathematically a trend and you can consider acting on it.
Recall that a key part of your analysis is the period of time you investigate; in our example, one window of time yielded a mathematical trend, while the other window of time for the exact same data did not. Choose a period of time that’s relevant and appropriate to what you’re trying to accomplish with the data. In our example, a 5-year retrospective would be appropriate for a big picture landscape of social media, while a 1-year retrospective would be appropriate for something like annual planning.
For questions that are bigger and riskier, you’ll want to investigate more sophisticated techniques for determining whether something is a trend or not, such as the Mann-Kendall test. You’ll also want to use different kinds of regression based on the data you’re working with; some forms of data lend themselves to more advanced regressions. However, for just getting started, the results of a simple linear regression are good enough for now.
Remember that the value of trend analysis isn’t just determining whether something is a trend or not; the value comes from the decisions you make and the actions you take once you know.
You might also enjoy:
- Mind Readings: Generative AI and Addition vs Substitution of Jobs
- Almost Timely News, January 14, 2024: The Future of Generative AI is Open
- Almost Timely News, January 7, 2024: Should You Buy a Custom GPT?
- Mind Readings: What Makes A Good Conference/Event?
- Mind Readings: Hacking Social Media Algorithms
Want to read more like this from Christopher Penn? Get updates here:
 Take my Generative AI for Marketers course! |

Leave a Reply